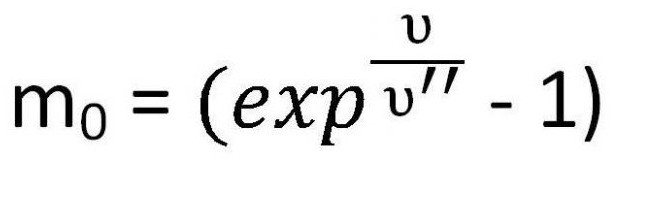Формула циолкоцфвского

Отличие реальной скорости ракеты от характеристической

Поскольку в условиях реального полёта на ракету кроме тяги двигателей действуют и другие силы, скорость, развиваемая ракетами в этих условиях, как правило, ниже характеристической из-за потерь, вызываемых силами гравитации, сопротивления среды и другими факторами.

В следующей таблице приведён баланс скоростей ракеты Сатурн V при выводе корабля Аполлон на траекторию полёта к Луне.

Ступень	Характеристическая скорость, м/c	Гравитационные потери, м/c	Аэродинамические потери, м/c	Потери на управление, м/c	Фактическая скорость, м/c
Первая (S-IC)	3660	1220	46	2394
Вторая (S-II)	4725	335	183	4207
Третья (S-IVB)	4120	122	4,5	3993,5
В сумме	12505	1677	46	187,5	10594,5

Как видно из таблицы, гравитационная составляющая является наибольшей в общей величине потерь. Гравитационные потери возникают из-за того, что ракета, стартуя вертикально, не только разгоняется, но и набирает высоту, преодолевая тяготение Земли, и на это также расходуется топливо. Величина этих потерь вычисляется по формуле:

Δvg =∫tg(t)⋅cos⁡(γ(t))dt,{\displaystyle \Delta v_{g}\ =\int \limits _{0}^{t}g(t)\cdot \cos(\gamma (t))\,dt,}

где g(t),{\displaystyle g(t),} γ(t){\displaystyle \gamma (t)} — местное ускорение гравитации и угол между вектором силы тяги двигателя и местным вектором гравитации, соответственно, являющиеся функциями времени по программе полёта.

Как видно из таблицы, наибольшая часть этих потерь приходится на участок полёта первой ступени. Это объясняется тем, что на этом участке траектория отклоняется от вертикали в меньшей степени, чем на участках последующих ступеней, и значение cos⁡(γ(t)){\displaystyle \cos(\gamma (t))} близко к максимальному значению — 1.

Аэродинамические потери вызваны сопротивлением воздушной среды при движении ракеты в ней и рассчитываются по формуле:

Δva =∫tA(t)m(t)dt,{\displaystyle \Delta v_{a}\ =\int \limits _{0}^{t}{\frac {A(t)}{m(t)}}\,dt,}

где A(t){\displaystyle A(t)} — сила лобового аэродинамического сопротивления;

m(t){\displaystyle m(t)} — текущая масса ракеты.

Основные потери от сопротивления воздуха также приходятся на участок работы 1-й ступени ракеты, так как этот участок проходит в нижних, наиболее плотных слоях атмосферы.

Космический аппарат должен быть выведен на орбиту со строго определёнными параметрами, для этого система управления на активном участке полёта разворачивает ракету по определённой программе, при этом направление тяги двигателя отклоняется от текущего направления движения ракеты, а это влечёт за собой потери скорости на управление, которые рассчитываются по формуле:

Δvu =∫tF(t)m(t)⋅(1−cos⁡(α(t)))dt,{\displaystyle \Delta v_{u}\ =\int \limits _{0}^{t}{\frac {F(t)}{m(t)}}\cdot (1-\cos(\alpha (t)))\,dt,}

где F(t){\displaystyle F(t)} — текущая сила тяги двигателя;

m(t){\displaystyle m(t)} — текущая масса ракеты, а α(t){\displaystyle \alpha (t)} — угол между векторами тяги и скорости ракеты.

Наибольшая часть потерь на управление ракеты приходится на участок полёта 2-й ступени, поскольку именно на этом участке происходит переход от вертикального полёта в горизонтальный, и вектор тяги двигателя в наибольшей степени отклоняется по направлению от вектора скорости ракеты.

Формула его имени

В 1892 году Циолковского перевели в Калугу. Скажем прямо: Калуге повезло! Если бы волею начальства Циолковский остался в Боровске, то сегодня этот город называли бы «колыбелью отечественной космонавтики». Именно в Калуге учёный-самоучка совершил открытие, которое обессмертило его имя.

Хотя Константин Эдуардович продолжал плотно заниматься проектом металлического дирижабля, его всё сильнее интересовали вопросы межпланетных перелётов. Например, он пытался представить, какие эффекты будут наблюдаться в состоянии невесомости. Однако Циолковский как практик хорошо видел и главную проблему, препятствующую освоению Солнечной системы, — отсутствие технической возможности разогнаться до космических скоростей. Описанные в фантастике концепции лунных пушек и антигравитационных аппаратов выглядели пустым фантазированием, поскольку нарушали известные законы физики.

Константин Циолковский за работой

На решение проблемы Циолковского навела брошюра Александра Фёдорова «Новый принцип воздухоплавания, исключающий воздух как опорную среду», изданная в 1896 году. В ней молодой изобретатель описывал машину, которая сможет летать в безвоздушном пространстве, используя реактивную силу вытекающих из неё газов, фактически — ракету. Выкладки показались Константину Эдуардовичу туманными, и он сел за собственные расчёты.

Формула Циолковского была несовершенна, но и её на начальном этапе оказалось достаточно, чтобы провести анализ. Калужский учитель установил, что межпланетные полёты вполне возможны, если в качестве топлива применять смесь из нефти и жидкого кислорода — эти компоненты в его время добывать и использовать уже умели.

Циолковскому понадобилось время, чтобы осмыслить своё открытие и изложить его в виде статьи «Исследование мировых пространств реактивными приборами», которая была опубликована в мае 1903 года. Помимо обоснования выведенной формулы, калужский учитель приводил описание простейшей ракеты с двигателем на жидком топливе, которая могла бы доставить человека до Луны и дальше. Какого было его удивление, когда научный мир проигнорировал публикацию.

10 мая 1897 года Циолковский вывел формулу, которая сегодня носит его имя. Она связывает четыре параметра: скорость ракеты в любой момент времени, скорость истечения продуктов сгорания из сопла, массу ракеты и массу взрывных веществ. Значение этой формулы для инженера-ракетчика трудно переоценить. Допустим, необходимо запустить спутник на околоземную орбиту. Значит, скорость ракеты после исчерпания топлива должна равняться первой космической скорости. Скорость истечения для каждого вещества индивидуальна. Располагая этими двумя величинами, можно перебирать соотношения масс топлива и ракеты, добиваясь оптимального.

Тогда Циолковский написал вторую часть работы, которая увидела свет через восемь лет в журнале «Вестник воздухоплавания». В ней он привёл свои расчёты, связанные с преодолением силы земного тяготения и временем полёта к соседним планетам; здесь же выдвинул идею автономной системы жизнеобеспечения для космических кораблей. На этот раз статья Циолковского наделала много шума, и о калужском учителе начали писать в прессе. Однако лишь немногие понимали значение его работ. Чтобы разъяснить публике суть своих открытий, Константин Эдуардович прибегнул к фантастике.

Значение космонавтики для человечества

С середины прошлого века у человечества существенно расширились представления не только о нашей планете, но и о Вселенной в целом. Сами полеты, пусть пока и не столь отдаленные, открывают перспективы для людей в отношении исследования других планет и галактик.

С одной стороны, это кажется отдаленной перспективой, с другой, если сопоставить динамику развития технологий за последние десятилетия, то представляется возможным стать свидетелем и участником событий и современникам.

Благодаря освоению космоса появилась возможность взглянуть на некоторые привычные науки и дисциплины не просто более глубоко, но и абсолютно под другим углом, применять ранее неизвестные методы исследования.

Практическое космостроение способствовало быстрому освоению сложных техник, к которым бы не обратились при других обстоятельствах.

Сегодня космонавтика часть жизни каждого человека, даже если люди об этом не задумываются. Например, общение по мобильному телефону или просмотр спутникового телевидения доступны именно благодаря разработкам второй половины двадцатого века.

К основным направлениям изучения последних двадцати лет относятся: околоземное пространство, Луна и отдаленные планеты. Говоря о том, сколько лет космонавтике, будем вести отсчет от запуска первого спутника, а значит, шестьдесят один год в 2018 году.

Формула Циолковского

Формула для вычисления скорости ракеты, обнаружена в математических трудах Циолковского, написанных им в 1897 г.

,

где:

V — скорость летательного аппарата после выработки всего топлива:

I – отношение тяги двигателя к расходу топлива в секунду (величина, называемая удельным импульсом ракетного двигателя). Для теплового ракетного двигателя u = I.

M₁ – масса летательного аппарата в начальный момент полёта. Она включает массу самой конструкции ракеты, массу топлива и массу полезной нагрузки (например, космического корабля, который выводится ракетой на орбиту).

M₂ – масса летательного аппарата в конечный момент полёта. Так как топливо к этому времени уже израсходовано, то это будет масса конструкции + масса полезной нагрузки.

С помощью формулы Циолковского можно рассчитать количество топлива, необходимое ракете для получения заданной скорости.

Из формулы Циолковского получаем отношение начальной массы ракеты к её конечной массе:

Обозначим:

M_o– масса полезного груза

M_k — масса конструкции ракеты

M_t— масса топлива

Масса конструкции зависит от массы топлива. Чем больше топлива необходимо ракете, тем больше резервуаров потребуется для его транспортировки, а значит, большей будет и масса конструкции.

Отношение этих масс выражается формулой:

,

где k – коэффициент, который показывает количество топлива на единицу массы конструкции ракеты.

Этот коэффициент может быть разным в зависимости от того, какие материалы использованы в конструкции ракеты. Чем легче и прочнее эти материалы, тем меньшим будет коэффициент, и легче конструкция. Кроме того, он зависит и от плотности топлива. Чем плотнее топливо, тем меньшие по объёмы ёмкости потребуются для его транспортировки, и тем выше значение k.

Подставив в формулу Циолковского выражения начальной и конечной массы ракеты через массы конструкции, груза и топлива, получим:

Из этого выражения следует, что величина массы топлива равна:

Зная значение удельного импульса топлива и массу полезного груза, можно рассчитать скорость ракеты.

Эта формула имеет смысл только в том случае, если 

или 

Если это условие не выполняется, ракета никогда не сможет достигнуть заданной скорости.

Выйти из колыбели

Философские работы Константина Циолковского настолько расходились с государственной идеологией Советского Союза, что в течение десятилетий были попросту запрещены для публикации. Тем не менее его вариант космизма стал достоянием общества — опять же через фантастику. К примеру, в повести Александра Полещука «Ошибка инженера Алексеева», опубликованной в альманахе «Мир приключений. Книга шестая» (1961) не только приводились названия ключевых философских статей Циолковского («Воля Вселенной», «Любовь к самому себе, или Истинное себялюбие», «Причина Космоса»), но и цитировались большие фрагменты из них. Повесть была переиздана отдельной книгой под названием «Ошибка Алексея Алексеева», но её подвергли разгромной критике, обвиняя автора в приверженности «оккультизму».

Памятник Константину Циолковскому на Аллее космонавтов в Москве

Философию Константина Циолковского можно найти и в романе Владимира Щербакова «Семь стихий» (1980), который был даже экранизирован. Несомненным поклонником панпсихизма был фантаст Юрий Медведев, что отразилось в его повести «Комната невесты» (1983). Эти авторы вполне разделяли веру калужского учителя в существование высокоразвитых инопланетян, которые выращивают человечество, словно оранжерейный цветок, в надежде, что оно не окажется сорняком.

Надо признать, что философия Циолковского, оставаясь под негласным цензурным запретом, не оказала сколько-нибудь значимого влияния на развитие космонавтики. Зато оказало другое. В 1947 году талантливый ракетчик Михаил Тихонравов, используя работы Циолковского, посвящённые многоступенчатым ракетам, предложил идею «пакета», в котором ракетные ступени не ставятся друг на друга, а располагаются рядом. Идея очень понравилась Сергею Королёву, и через десять лет с казахстанского полигона, который впоследствии получил название «Байконур», стартовала баллистическая ракета Р-7, сконструированная по схеме «пакет». С помощью этой ракеты были запущены первые искусственные спутники Земли, первые межпланетные станции и первые космонавты. И сегодня более совершенные модификации ракеты Р-7 служат мировой космонавтике под названиями «Союз» и «Прогресс».

* * *

Константин Циолковский умер в Калуге 19 сентября 1935 года от рака желудка. За шесть дней до своей смерти он писал: «До революции моя мечта не могла осуществиться. Лишь Октябрь принёс признание трудам самоучки: лишь советская власть и партия Ленина — Сталина оказали мне действенную помощь. Я почувствовал любовь народных масс, и это давало мне силы продолжать работу, уже будучи больным… Все свои труды по авиации, ракетоплаванию и межпланетным сообщениям передаю партии большевиков и советской власти — подлинным руководителям прогресса человеческой культуры. Уверен, что они успешно закончат мои труды».

Не исключено, когда-нибудь философию Константина Циолковского забудут. Забудут, что он вывел ключевую формулу и придумал прообраз первой космической ракеты. Всё возможно. Однако можно быть уверенным, что в человеческой памяти навсегда останется его лозунг, содержащий суть космической экспансии:

Планета есть колыбель разума, но нельзя вечно жить в колыбели

Второй ракетный бум

Ракеты ждали своего часа и дождались: в 1920-х годах начался второй ракетный бум, и связан он в первую очередь с двумя именами.

Константин Эдуардович Циолковский — ученый-самоучка из Рязанской губернии,  невзирая на трудности и препятствия, сам дошел до многих открытий, без которых невозможно было бы даже говорить о космосе. Идея использования жидкого топлива, формула Циолковского, которая рассчитывает необходимую для полета скорость, исходя из соотношения конечной и начальной масс, многоступенчатая ракета — все это его заслуга. Во многом под влиянием его трудов создавалось и оформлялось отечественное ракетостроение. В Советском Союзе начали стихийно возникать общества и кружки по изучению реактивного движения, в числе которых ГИРД — группа изучения реактивного движения, а в 1933 году под патронажем властей появился Реактивный институт.

Второй герой ракетной гонки — немецкий физик Вернер фон Браун. Браун имел отличное образование и живой ум, а после знакомства с другим светилом мирового ракетостроения, Генрихом Обертом, он решил приложить все свои силы к созданию и усовершенствованию ракет. В годы Второй Мировой фон Браун фактически стал отцом «оружия возмездия» Рейха — ракеты «Фау-2», которую немцы начали применять на поле боя в 1944 году. «Крылатый ужас», как называли её в прессе, принес разрушение многим английским городам, но, к счастью, на тот момент крах нацизма был уже делом времени. Вернер фон Браун вместе со своим братом решил сдаться в плен к американцам, и, как показала история, это был счастливый билет не только и не столько для ученых, сколько для самих американцев. С 1955 года Браун работает на американское правительство, и его изобретения ложатся в основу космической программы США.

Но вернемся в 1930-е. Советское правительство по достоинству оценило рвение энтузиастов на пути к космосу и решило употребить его в своих интересах. В годы войны себя отлично показала «Катюша» — система залпового огня, которая стреляла реактивными ракетами. Это было во многом инновационное оружие: «Катюша» на базе легкого грузовика «Студебеккер» приезжала, разворачивалась, обстреливала сектор и уезжала, не давая немцам опомниться.

Окончание войны подкинуло нашему руководству новую задачу: американцы продемонстрировали миру всю мощь ядерной бомбы, и стало совершенно очевидно, что на статус сверхдержавы может претендовать только тот, у кого есть нечто похожее. Но здесь была проблема. Дело в том, что, помимо самой бомбы, нам нужны были средства доставки, которые бы смогли обойти ПВО США. Самолеты для этого не годились. И СССР решил сделать ставку на ракеты.

Константин Эдуардович Циолковский умер в 1935 году, но ему на смену пришло целое поколение молодых ученых, которое и отправило человека в космос. Среди этих ученых был Сергей Павлович Королев, которому суждено было стать «козырем» Советов в космической гонке.

СССР принялся за создание своей межконтинентальной ракеты со всем усердием: были организованы институты, собраны лучшие ученые, в подмосковных Подлипках создается НИИ по ракетному вооружению, и работа кипит вовсю.

Только колоссальное напряжение сил, средств и умов позволило Советскому Союзу в кратчайшие сроки построить свою ракету, которую назвали Р-7. Именно её модификации вывели в космос «Спутник» и Юрия Гагарина, именно Сергей Королев и его соратники дали старт космической эре человечества. Но из чего состоит космическая ракета?

Другая форма формулы

В некоторых ресурсах применяется несколько иная формула Циолковского, уравнение, в котором вместо υ′ применяется другой параметр — I. В данном случае I называют удельным импульсом, и даже приводится объяснение, что удельный импульс выражается через тягу двигателя и его сжиганию массы топлива за единицу времени. Первый вопрос, который приходит на ум — вопрос о размерности. В отличие от скорости, импульс имеет другую размерность, которая будет противоречить сути формулы. Однако, непосредственно удельный импульс совпадает по размерности со скоростью.

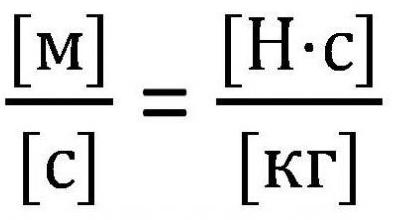
Удельный импульс показывает количество секунд, при котором двигатель, истратив единицу топлива, получит единицу силы. Применяется сугубо в описании реактивного двигателя.

История

Один из первых эскизов многоступенчатой ракеты был представлен в 1556 году в книге военного техника Конрада Хааса. В XVII веке рисунок с изображением ракет был опубликован в труде военного инженера и генерала от артиллерии Казимира Семеновича, «Artis Magnae Artilleriae pars prima» (лат.  «Великое искусство артиллерии часть первая»), напечатанном в 1650 году в Амстердаме, Нидерланды. На нём — трехступенчатая ракета, в которой третья ступень вложена во вторую, а обе они вместе — в первую ступень. В головной части помещался состав для фейерверка. Ракеты были начинены твёрдым топливом — порохом. Это изобретение интересно тем, что оно более трёхсот лет назад предвосхитило направление, по которому пошла современная ракетная техника.

Впервые идея использования многоступенчатых ракет была выдвинута американским инженером Робертом Годдардом в 1914 году, и был получен патент на изобретение. В г. К. Э. Циолковский выпустил в свет свою новую книгу под заглавием «Космические ракетные поезда». Этим термином К. Циолковский назвал составные ракеты или, вернее, агрегат ракет, делающих разбег по земле, потом в воздухе и, наконец, в космическом пространстве. Поезд, составленный, например, из 5 ракет, ведётся сначала первой — головной ракетой; по использовании её горючего, она отцепляется и сбрасывается на землю. Далее, таким же образом, начинает работать вторая, затем третья, четвёртая и, наконец, пятая, скорость которой будет к тому времени достаточно велика, чтобы унестись в межпланетное пространство. Последовательность работы с головной ракеты вызвана стремлением заставить материалы ракет работать не на сжатие, а на растяжение, что позволит облегчить конструкцию. По Циолковскому, длина каждой ракеты — 30 метров. Диаметры — 3 метра. Газы из сопел вырываются косвенно к оси ракет, чтобы не давить на следующие ракеты. Длина разбега по земле — несколько сот километров.

Несмотря на то, что в технических деталях ракетостроение пошло во многом по другому пути (современные ракеты, например, не «разбегаются» по земле, а взлетают вертикально, и порядок работы ступеней современной ракеты — обратный, по отношению к тому, о котором говорил Циолковский), сама идея многоступенчатой ракеты и сегодня остаётся актуальной.

В 1935 году Циолковский написал работу «Наибольшая скорость ракеты», в которой утверждал, что при уровне технологии того времени достичь первой космической скорости (на Земле) можно только с помощью многоступенчатой ракеты. Это утверждение сохраняет свою справедливость и сегодня: все современные носители космических аппаратов — многоступенчатые. Первым рукотворным объектом, пересекшим линию Кармана и вышедшим в космос, была одноступенчатая немецкая ракета Фау-2. Высота полётов достигала 188 км.

Исаак Ньютон (1642 – 1727)

Работы Исаака Ньютона в области физики и математики стали неизмеримо важными для современных знаний о космосе. Его три универсальных закона движения легли в основу физики, а его работы в исчислении дали огромный толчок этой области. Ньютон доказал оба кеплеровских закона планетарного движения и гелиоцентрическую природу Солнечной системы. Также он разработал первый практический отражающий телескоп. Его работа в изучении гравитации сыграла важную роль в развитии будущих теорий в области астрофизики. Короче говоря, вся физика, которая помогает нам запускать полезный груз в космос и точно знать его поведение по прибытии в пункт назначения, началась с работ Исаака Ньютона.

Межпланетные корабли

В Советской России из Константина Циолковского сделали культовую фигуру. Он идеально подходил на роль «самородка», которого не понимали при царизме и который обрёл признание в стране раскрепощённого труда. Ему даже была назначена пожизненная пенсия за заслуги перед наукой и прогрессом.

С большим пиететом относились к Циолковскому и ракетчики. Будущий главный конструктор ракетно-космической техники Сергей Королёв понимал, что для создания новой сферы научно-технической деятельности, какой станет реальная космонавтика, ему нужны авторитетные предшественники. Но, кроме Циолковского, в России никого подходящего не было. Поэтому, едва занявшись ракетостроением, Королёв установил тесные контакты с калужским учителем, цитировал его труды и всячески чествовал.

Ссылаясь на Циолковского, молодые советские ракетчики преодолели недоверие высокопоставленных военных и развернули работу — сначала в Группе по изучению реактивного движения (ГИРД), затем в Реактивном научно-исследовательском институте (РНИИ).

В первой повести, которая рассказывает о попытке капиталистов пережить мировую революцию на Венере, идеи Циолковского описаны лишь во вводной части, где речь идёт о подготовке ракетного «Ковчега» к старту. А вот «Звезду КЭЦ» можно назвать панегириком калужскому учителю, ведь в ней охвачены практически все его мечты — от воздухоплавания до построения утопического общества, преобразующего мир за счёт космических ресурсов. Изначально повесть называлась «Вторая Луна», однако Александр Беляев переименовал её в память о Циолковском после его смерти.

Огромный интерес к работам Циолковского проявляли популяризаторы и писатели-фантасты. Ведь его работы доказывали, что невероятные мечты скоро смогут стать реальностью. Со стороны популяризаторов с Циолковским работал знаменитый Яков Перельман, который написал на основе его идей книгу «Межпланетные путешествия», выдержавшую десять переизданий. Со стороны фантастов — Александр Беляев. При участии калужского учителя он написал две повести — «Прыжок в ничто» (1933) и «Звезда КЭЦ» (1936).

Кадр из фильма «Космический рейс»

Помимо прочего, калужский учитель выступил научным консультантом немого полнометражного фильма «Космический рейс» (1936), снятого талантливым режиссёром «Мосфильма» Василием Журавлёвым при поддержке великого Сергея Эйзенштейна. Создатели киноленты нуждались в достоверном описании эффектов, которые будут наблюдаться в кабине космического корабля при полёте и высадке на Луну, а получить такую информацию от кого-либо другого было попросту невозможно. Хотя далеко не все рекомендации Циолковского киношники приняли к сведению, «Космический рейс» считается одним из наиболее достоверных фильмов с точки зрения законов физики.

Отличие реальной скорости ракеты от характеристической

Поскольку в условиях реального полёта на ракету кроме тяги двигателей действуют и другие силы, скорость, развиваемая ракетами в этих условиях, как правило, ниже характеристической из-за потерь, вызываемых силами гравитации, сопротивления среды и другими факторами.

В следующей таблице приведён баланс скоростей ракеты Сатурн V при выводе корабля Аполлон на траекторию полёта к Луне.

Ступень	Характеристическая скорость, м/c	Гравитационные потери, м/c	Аэродинамические потери, м/c	Потери на управление, м/c	Фактическая скорость, м/c
Первая (S-IC)	3660	1220	46	2394
Вторая (S-II)	4725	335	183	4207
Третья (S-IVB)	4120	122	4,5	3993,5
В сумме	12505	1677	46	187,5	10594,5

Как видно из таблицы, гравитационная составляющая является наибольшей в общей величине потерь. Гравитационные потери возникают из-за того, что ракета, стартуя вертикально, не только разгоняется, но и набирает высоту, преодолевая тяготение Земли, и на это также расходуется топливо. Величина этих потерь вычисляется по формуле:

Δvg =∫tg(t)⋅cos⁡(γ(t))dt,{\displaystyle \Delta v_{g}\ =\int \limits _{0}^{t}g(t)\cdot \cos(\gamma (t))\,dt,}

где g(t),{\displaystyle g(t),} γ(t){\displaystyle \gamma (t)} — местное ускорение гравитации и угол между вектором силы тяги двигателя и местным вектором гравитации, соответственно, являющиеся функциями времени по программе полёта.

Как видно из таблицы, наибольшая часть этих потерь приходится на участок полёта первой ступени. Это объясняется тем, что на этом участке траектория отклоняется от вертикали в меньшей степени, чем на участках последующих ступеней, и значение cos⁡(γ(t)){\displaystyle \cos(\gamma (t))} близко к максимальному значению — 1.

Аэродинамические потери вызваны сопротивлением воздушной среды при движении ракеты в ней и рассчитываются по формуле:

Δva =∫tA(t)m(t)dt,{\displaystyle \Delta v_{a}\ =\int \limits _{0}^{t}{\frac {A(t)}{m(t)}}\,dt,}

где A(t){\displaystyle A(t)} — сила лобового аэродинамического сопротивления;

m(t){\displaystyle m(t)} — текущая масса ракеты.

Основные потери от сопротивления воздуха также приходятся на участок работы 1-й ступени ракеты, так как этот участок проходит в нижних, наиболее плотных слоях атмосферы.

Космический аппарат должен быть выведен на орбиту со строго определёнными параметрами, для этого система управления на активном участке полёта разворачивает ракету по определённой программе, при этом направление тяги двигателя отклоняется от текущего направления движения ракеты, а это влечёт за собой потери скорости на управление, которые рассчитываются по формуле:

Δvu =∫tF(t)m(t)⋅(1−cos⁡(α(t)))dt,{\displaystyle \Delta v_{u}\ =\int \limits _{0}^{t}{\frac {F(t)}{m(t)}}\cdot (1-\cos(\alpha (t)))\,dt,}

где F(t){\displaystyle F(t)} — текущая сила тяги двигателя;

m(t){\displaystyle m(t)} — текущая масса ракеты, а α(t){\displaystyle \alpha (t)} — угол между векторами тяги и скорости ракеты.

Наибольшая часть потерь на управление ракеты приходится на участок полёта 2-й ступени, поскольку именно на этом участке происходит переход от вертикального полёта в горизонтальный, и вектор тяги двигателя в наибольшей степени отклоняется по направлению от вектора скорости ракеты.

Валентин Глушко (1908 – 1989)

Мало кто знает, что Валентин Глушко, крупнейший советский ученый в области ракетно-космической техники, был одним из пионеров в этой области, а его деятельность положила начало отечественному жидкостному ракетному двигателестроению. Подробнее о твердотопливных и жидкотопливных ракетных двигателях можно почитать здесь. C 1977 года Глушко был генеральным конструктором легендарного НПО «Энергия».

На счету изобретений и конструкций, в создании которых Глушко принимал непосредственное участие, — первый в мире электротермический ракетный двигатель (1928–1933), первый советский жидкостный ракетный двигатель ОРМ (1930–1931), семейство ракет РЛА на жидком топливе (1932–1933) и мощные жидкостные ракетные двигатели, которые ставили практически на все отечественные ракеты, летавшие в космос до настоящего момента. Эти двигатели выводили на орбиту первый и последующие спутники Земли, космические корабли с Юрием Гагариным и другими космонавты, а также участвовали в полетах к Луне и планетам Солнечной системы. Базовый блок орбитальной станции «Мир» также был разработан Глушко. Этот человек внес и колоссальный личный вклад в мировую науку, благодаря многолетним работам по созданию фундаментальных справочников по термическим константам, термодинамическим и теплофизическим свойствам различных веществ и другим.

Вывод формулы Циолковского

Необходимо вывести формулу, описывающую движение тела с переменной массой. Формула Циолковского таковой и является. Вывод представлен ниже.

В данных вычислениях считается, что на движущееся тело не действуют внешние силы, то есть F = 0.

Тогда mdυ = υ′′dm

Так как воздействие внешних сил на летящую ракету равно нулю, то она движется прямолинейно, а скорость движения противоположно направлена скорости выхода газа. Соответственно, υ = -υ′′

Получается выражение, которое необходимо проинтегрировать.

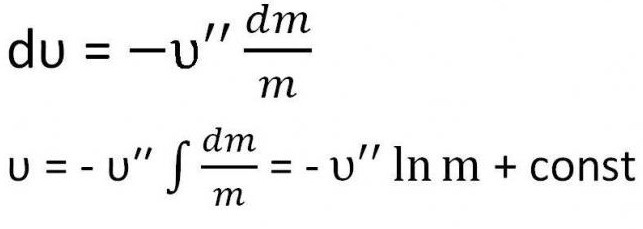
Необходимо найти константу. Для этого достаточно подставить в уравнение начальные условия — скорость равна нулю, а масса — сумме массы топлива и массы ракеты (m + m)

Вообще говоря, m в формуле складывается из двух параметров — из полезной нагрузки и конструкции ракеты. Полезной нагрузкой называется общая масса груза и экипажа.

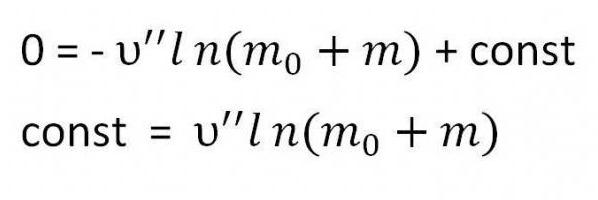
Подставляем найденную константу в формулу. В результате и получается выражение искомой формулы.

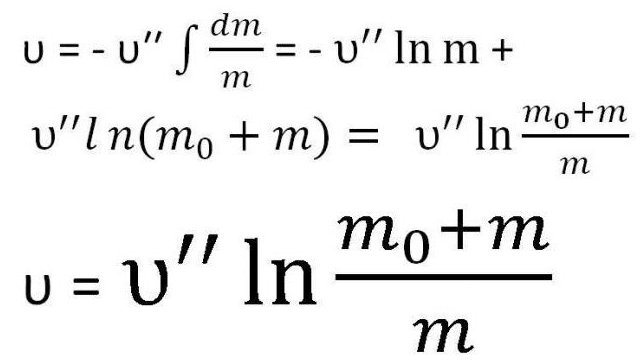
Это и есть один из вариантов формулы Циолковского для скорости

Однако иногда необходимо принять во внимание именно массу. Поэтому ее иногда записывают следующим образом:

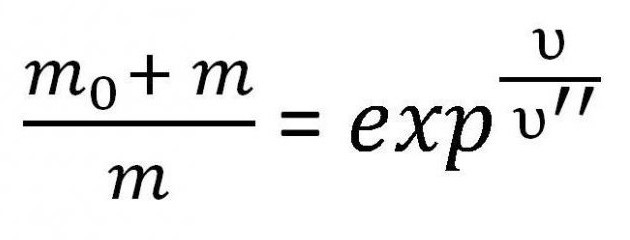
Данная формула используется для расчета массы топлива, которая требуется для развития определенной скорости при заданных условиях.

Рассмотрю далее небольшую задачу. Предположим, ракете необходимо развить первую космическую скорость для вращения по орбите Земли. Тогда для этого необходимо в первую очередь рассчитать массу топлива, конечно же. Тогда ее очень просто выразить из формулы Циолковского.